How accurate are our predictions?

by Javier Prieto, Aaron Gertler
Share

 

When investigating a grant, Open Philanthropy staff often make probabilistic predictions about grant-related outcomes they care about, e.g. “I’m 70% confident the grantee will achieve milestone #1 within 1 year.” This allows us to learn from the success and failure of our past predictions and get better over time at predicting what will happen if we make one grant vs. another, pursue one strategy vs. another, etc. We hope that this practice will help us make better decisions and thereby enable us to help others as much as possible with our limited time and funding.[1]

Thanks to the work of many people, we now have some data on our forecasting accuracy as an organization. In this blog post, I will:

  1. Explain how our internal forecasting works. [more]
  2. Present some key statistics about the volume and accuracy of our predictions. [more]
  3. Discuss several caveats and sources of bias in our forecasting data: predictions are typically scored by the same person that made them, our set of scored forecasts is not a random or necessarily representative sample of all our forecasts, and all hypotheses discussed here are exploratory. [more]

1. How we make and check our forecasts

Grant investigators at Open Philanthropy recommend grants via an internal write-up. This write-up typically includes the case for the grant, reservations and uncertainties about it, and logistical details, among other things. One of the (optional) sections in that write-up is reserved for making predictions.

The prompt looks like this (we’ve included sample answers):

Do you have any new predictions you’re willing to make for this grant? […] A quick tip is to scan your write-up for expectations or worries you could make predictions about. […]

Predictions Scoring (you can leave this blank until you’re able to score)
With X% confidence… …I predict that (yes/no or confidence interval prediction)… …by time Y (ideally a date, not e.g. “in one year”) Score (please stick to True / False / Not Assessed) Comments or caveats about your score
30% The grantee will produce outcome Z End of 2021  

 

After a grant recommendation is submitted and approved, the predictions in that table are logged into our Salesforce database for future scoring (as true or false). If the grant is renewed, scoring typically happens during the renewal investigation phase, since that’s when the grant investigator will be collecting information about how the original grant went. If the grant is not renewed, grant investigators are asked to score their predictions after they come due.[2] Scores are then logged into our database, and that information is used to produce calibration dashboards for individual grant investigators and teams of investigators working in the same focus area. 

A user’s calibration dashboard (in Salesforce) looks like this:

 

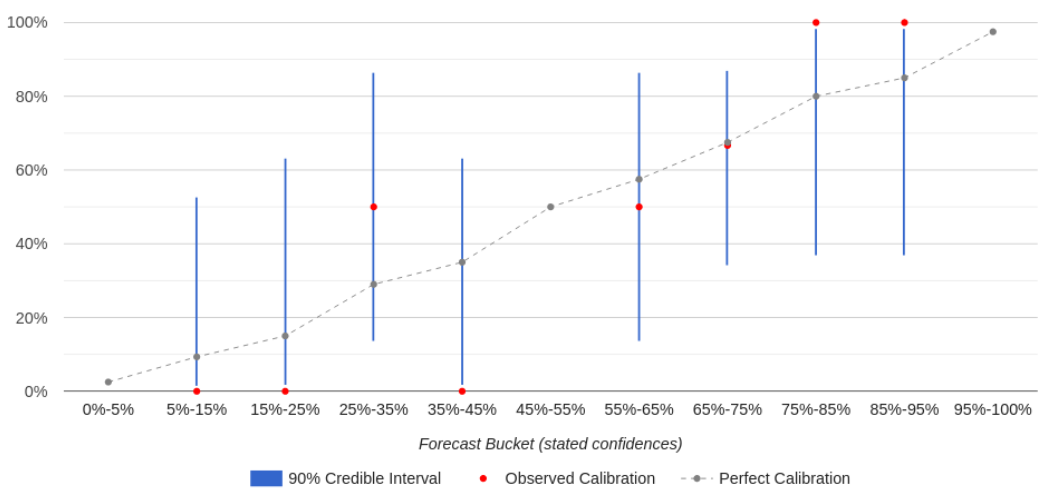
The calibration curve tells the user where they are well-calibrated vs. overconfident vs. underconfident. If a forecaster is well-calibrated for a given forecast “bucket” (e.g. forecasts they made with 65%-75% confidence), then the percent of forecasts that resolved as “true” should match that bucket’s confidence level (e.g. they should have come true 65%-75% of the time). On the chart, their observed calibration (the red dot) should be close to perfect calibration (the gray dot) for that bucket.[3] If it’s not, then the forecaster may be overconfident or underconfident for that bucket — for example, if things they predict with 65%-75% confidence happen only 40% of the time (overconfidence). (A bucket can also be empty if the user hasn’t made any forecasts within that confidence range.)

Each bucket also shows a 90% credible interval (the blue line) that indicates how strong the evidence is that the forecaster’s calibration in that bucket matches their observed calibration, based on how many predictions they’ve made in that bucket. As a rule of thumb, if the credible interval overlaps with the line of perfect calibration, that means there’s no strong evidence that they are miscalibrated in that bucket. As a user makes more predictions, the blue lines shrink, giving that user a clearer picture of their calibration.

In the future, we hope to add more features to these dashboards, such as more powerful filters and additional metrics of accuracy (e.g. Brier scores).

2. Results

2.1 Key takeaways

  1. We’ve made 2850 predictions so far. 743 of these have come due and been scored as true or false. [more]
  2. Overall, we are reasonably well-calibrated, except for being overconfident about the predictions we make with 90%+ confidence. [more]
  3. The organization-wide Brier score (measuring both calibration and resolution) is .217, which is somewhat better than chance (.250). This requires careful interpretation, but in short we think that our reasonably good Brier score is mostly driven by good calibration, while resolution has more room for improvement (but this may not be worth the effort). [more]
  4. About half (49%) of our predictions have a time horizon of ≤2 years, and only 13% of predictions have a time horizon of ≥4 years. There’s no clear relationship between accuracy and time horizon, suggesting that shorter-range forecasts aren’t inherently easier, at least among the short- and long-term forecasts we’re choosing to make. [more]

2.2 How many predictions have we made?

As of March 16, 2022, we’ve made 2850 predictions. Of the 1345 that are ready to be scored, we’ve thus far assessed 743 of them as true or false. (Many “overdue” predictions will be scored when the relevant grant comes up for renewal.) Further details are in a footnote.[4]

What kinds of predictions do we make? Here are some examples:

  • “[20% chance that] at least one human challenge trial study is conducted on a COVID-19 vaccine candidate [by Jul 1, 2022]”
  • “[The grantee] will play a lead role… in securing >20 new global cage-free commitments by the end of 2019, improving the welfare of >20M hens if implemented”
  • “[70% chance that] by Jan 1, 2018, [the grantee] will have staff working in at least two European countries apart from [the UK]”
  • “60% chance [the grantee] will hire analysts and other support staff within 3 months of receiving this grant and 2-3 senior associates and a comms person within 6-9 months of receiving this grant”
  • “70% chance that the project identifies ~100 geographically diverse advocates and groups for re-grants”
  • “[80% chance that] we will want to renew [this grant]”
  • “75% chance that [an expert we trust] will think [the grantee’s] work is ‘very good’ after 2 years”

Some focus areas[5] are responsible for most predictions, but this is mainly driven by the number of grant write-ups produced for each focus area. The number of predictions per grant write-up ranges from 3 to 8 and is similar across focus areas. Larger grants tend to have more predictions attached to them. We averaged about 1 prediction per $1 million moved, with significant differences across grants and focus areas.

2.3 Calibration

Good predictors should be calibrated. If a predictor is well-calibrated, that means that things they expect to happen with 20% confidence do in fact happen roughly 20% of the time, things they expect with 80% confidence happen roughly 80% of the time, and so on.[6] Our organization-wide calibration curve looks like this:

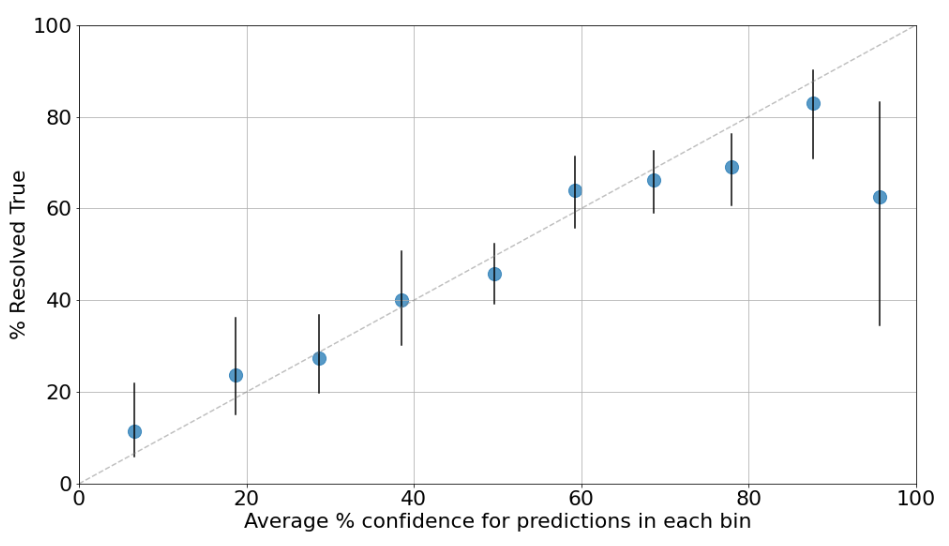
To produce this plot, prediction confidences were binned in 10% increments. For example, the leftmost dot summarizes all predictions made with 0%-10% confidence. It appears at the 6% confidence mark because that’s the average confidence of predictions in the 0%-10% range, and it shows that 12% of those predictions came true. The dashed gray line represents perfect calibration.

The vertical black lines are 90% credible intervals around the point estimates for each bin. If the bar is wider, that generally means we’re less sure about our calibration for that confidence range because we have fewer data points in that confidence range.[7] All the bins have at least 40 resolved predictions except the last one, which only has 8 – hence the wider interval. A table with the number of true / false predictions in each bin can be found in a footnote.[8]

The plot shows that Open Philanthropy is reasonably well-calibrated as a whole, except for predictions we made with 90%+ confidence (those events only happened slightly more than half the time) and possibly also in the 70%-80% range (those events happened slightly less than 70% of the time). In light of this, the “typical” Open Phil predictor should be less bold and push predictions that feel “almost certain” towards a lower number.[9]

2.4 Brier scores and resolution

On top of being well calibrated, good predictors should give high probability to events that end up happening and low probability to events that don’t. This isn’t captured by calibration. For example, imagine a simplified world in which individual stocks go up and down in price but the overall value of the stock market stays the same, and there aren’t any trading fees. In this world, one way to be well-calibrated is to make predictions about whether randomly chosen stocks will go up or down over the next month, and for each prediction just say “I’m 50% confident it’ll go up.” Since a randomly chosen stock will indeed go up over the next month about 50% of the time (and down the other 50% of the time), you’ll achieve perfect calibration! This good calibration will spare you from the pain of losing money, but it won’t help you make any money either. However, you will make lots of money if you can predict with 60% (calibrated) confidence which stocks will go up vs. down, and you’ll make even more money if you can predict with 80% calibrated confidence which stocks will go up vs. down. If you could do that, then your stock predictions would be not just well-calibrated but also have good “resolution.” 

A metric that captures both aspects of what makes a good predictor is the Brier score (also explained in the addendum at the end of this post). The most illustrative examples are:

  1. A perfect predictor (100% confidence on things that happen, 0% confidence on things that don’t) would get a Brier score of 0.
  2. A perfect anti-predictor (0% confidence on things that happen, 100% confidence on things that don’t) would get a score of 1.
  3. A predictor that always predicts 50% would get a score of 0.25 (assuming the events they predict happen half the time). Thus, a score higher than 0.25 means someone’s accuracy is no better than if they simply guessed 50% for everything.

The mean Brier score across all our predictions is 0.217, and the median is 0.160. (Remember, lower is better.) 75% of focus area Brier scores are under 0.25 (i.e. they’re better than chance).[10] 

This rather modest[11] Brier score together with overall good calibration implies our forecasts have low resolution.[12] Luke’s intuition on why there’s a significant difference in performance between these two dimensions of accuracy is that good calibration can probably be achieved through sheer reflection and training, just by being aware of the limits of one’s own knowledge, whereas resolution requires gathering and evaluating information about the topic at hand and carefully using it to produce a quantified forecast, something our grant investigators aren’t typically doing in much detail (most of our forecasts are produced in seconds or minutes). If this explanation is right, getting better Brier scores would require spending significantly more time on each forecast. We’re uncertain whether this would be worth the effort, since calibration alone can be fairly useful for decision-making and is probably much less costly to achieve, and our grant investigators have many other responsibilities besides making predictions.

2.5 Longer time horizons don’t hurt accuracy

Almost half of all our predictions are made less than 2 years before they will resolve (e.g. the prediction might be “X will happen within two years”),[13] with ~75% being less than 3 years out. Very few predictions are about events decades into the future.

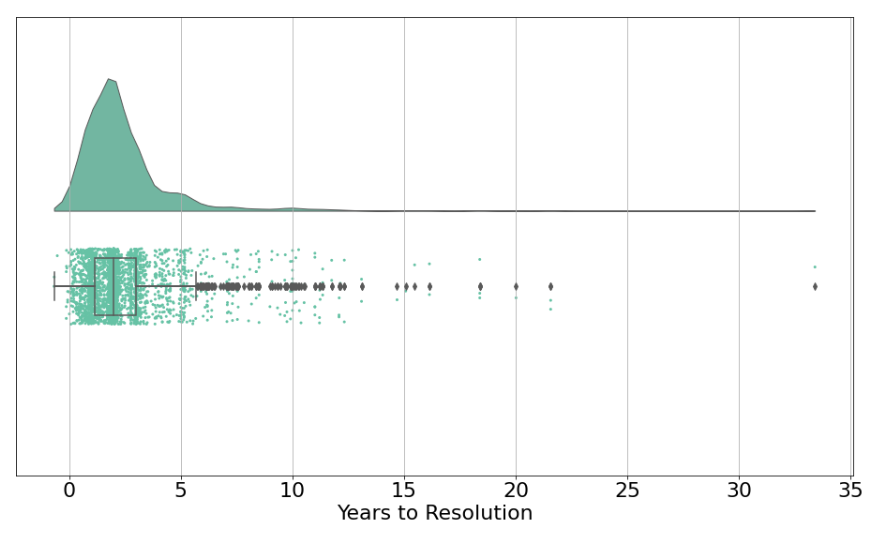
It’s reasonable to assume that (all else equal) the longer the time horizon, the harder it is to make accurate predictions.[14] However, our longer-horizon forecasts are about as accurate as our shorter-horizon forecasts.

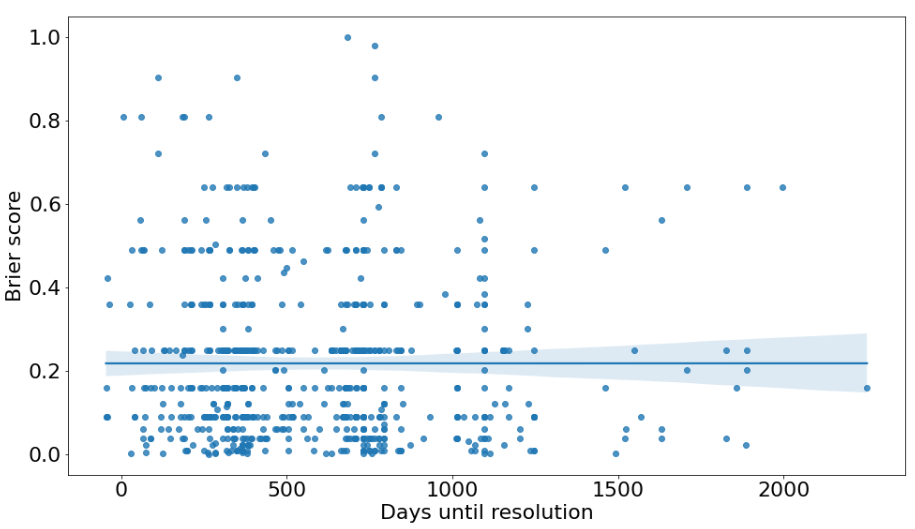
A possible explanation is question selection. Grant investigators may be less willing to produce long-range forecasts about things that are particularly hard to predict because the inherent uncertainty looks insurmountable. This may not be the case for short-range forecasts, since for these most of the information is already available.[15] In other words, we might be choosing which specific things to forecast based on how difficult we think they are to forecast regardless of their time horizon, which could explain why our accuracy doesn’t vary much by time horizon.

3. Caveats and sources of bias

There are several reasons why our data and analyses could be biased. While we don’t think these issues undermine our forecasting efforts entirely, we believe it’s important for us to explain them in order to clarify how strong the evidence is for any of our claims. The main issues we could identify are:

  1. Predictions are typically written and then later scored by the same person, because the grant investigator who made each prediction is typically also our primary point of contact with the relevant grantee, from whom we typically learn which predictions came true vs. false. This may introduce several biases. For example, predictors may choose events that are inherently easier to predict. Or, they may score ambiguous predictions in a way that benefits their accuracy score. Both things could happen subconsciously.
  2. There may be selection effects on which predictions have been scored. For example, many predictions have overdue scores, i.e. they are ready to be evaluated but have not been scored yet. The main reason for this is that some predictions are associated with active grants, i.e. grants that may be renewed in the future. When this happens, our current process is to leave them unscored until the grant investigator writes up the renewal, during which they are prompted to score past predictions. It shouldn’t be assumed that these unscored predictions are a random sample of all predictions, so excluding them from our analyses may introduce some hard-to-understand biases.
  3. The analyses presented here are completely exploratory. All hypotheses were put forward after looking at the data, so this whole exercise should be better thought of as “narrative speculations” rather than “scientific hypothesis testing.”

 

Addendum: Defining the Brier score

For binary events, the Brier score can be defined as

\( BS\,=\,\frac{1}{n} \sum_{i=1}^n (P_i\,-\,Y_i)^2 \)

 

Where \( i = 1,…,N \) ranges over events, \( p_i \) is the forecasted probability that the i-th event resolves True, and \( Y_i \) is the actual outcome of the i-th event (1 if True, 0 if False). A predictor that knows the base rate, b, of future events and predicts that on every event gets a Brier score of b * (1 – b). For example, if b = 50% (as is roughly the case for us), the expected Brier is 0.25. A perfect predictor (100% confidence on things that happen, 0% confidence on things that don’t) would get a Brief score of 0. A predictor that is perfectly anticorrelated with reality (predicts the exact opposite as a perfect predictor) would get a score of 1.

The Brier score can be decomposed into a sum of 3 components as

\( BS\,=\,E(p\, -\,P[Y|p])^2\,-\,E(P[Y|p]\,-\,b)^2\,+\,b\,*\,(1\,-\,b) \)

 

Where \( i = 1 \) denotes expectation, \( p_i \) is the forecasted probability of the event \(Y\), \(P[Y|p]\) is the actual probability of \(Y\) given that the forecasted probability was \(p\), and \(b\) is the base rate of \(Y\). The components can be interpreted as follows:

  1. The first one measures miscalibration. It is the mean squared error between forecasted and actual probabilities. It ranges from 0 (perfect calibration) to 1 (worst).
  2. The second one measures resolution. It is the expected improvement of one’s forecasts over the blind strategy that always outputs the base rate. It ranges from 0 (worst) to b(1-b) (best).
  3. The third one measures the inherent uncertainty of the events being forecasted. It is just the entropy of a binary event that happens with probability b.

In practice, because it is unlikely that any two events have the same forecasted probability, \(P[Y | p]\) is calculated by binning forecasts and averaging within each bin, i.e. the empirical estimate is \(P[Y | p]\) = (# of true predictions in that bin) / (total # of predictions in that bin). This is exactly what we do in our dashboards.

Footnotes

  1. [1] Here is a fuller list of reasons we make explicit quantified forecasts and later check them for accuracy, as described in an internal document by Luke Muehlhauser:

    1. There is some evidence that making and checking quantified forecasts can help you improve the accuracy of your predictions over time, which in theory should improve the quality of our grantmaking decisions (on average, in the long run).
    2. Quantified predictions can enable clearer communication between grant investigators and decision-makers. For example, if you just say it "seems likely" the grantee will hit their key milestone, it's unclear whether you mean a 55% chance or a 90% chance.
    3. Explicit quantified predictions can help you assess grantee performance relative to initial expectations, since it's easy to forget exactly what you expected them to accomplish, and with what confidence, unless you wrote down your expectations when you originally made the grant.
    4. The impact of our work is often difficult to measure, so it can be difficult for us to identify meaningful feedback loops that can help us learn how to be more effective and hold ourselves accountable to our mission to help others as much as possible. In the absence of clear information about the impact of our work (which is often difficult to obtain in a philanthropic setting), we can sometimes at least learn how accurate our predictions were and hold ourselves accountable to that. For example, we might never know whether our grant caused a grantee to succeed at X and Y, but we can at least check whether the things we predicted would happen did in fact happen, with roughly the frequencies we predicted.

  2. [2] In some rare cases, it’s possible for the people managing the database to score predictions using information available to them. However, predictions tend to be very in-the-weeds, so scoring them typically requires input from the grant investigators who made them.

  3. [3] The horizontal coordinate of the gray dots is calculated by averaging the confidence of all the predictions in each bin. Note that this is in general different from the midpoint of the bin; for example, if there are only two predictions in the 45%-55% bin and they have 46% and 48% confidence, respectively, then the point of perfect calibration in that bin would be 47%, not 50%.

  4. [4] Our stats as of 2022-03-16 are as follows (italics means the percentage is taken over scored predictions, not total):

    Status Number %
    Scored True 382 45%
    False 361 42%
    Not Assessed 115 13%
    Total Scored 858 30%
    Not scored Not Yet Due 1,448 51%
    Overdue 487 17%
    Missing End Date 57 2%
    Total Not Scored 1992 70%
    Total 2850 100%
    Some categories in the table above deserve further comments:
    • Not Assessed: There are several reasons why some predictions are not assessed:
      • Some predictions had vague / subjective resolution criteria (so that it was unclear whether the event happened or not).
      • We didn't check some predictions because it would have taken too much time or effort to do so.
      • Some predictions were premised on a condition that wasn't fulfilled (e.g. "if X happens, the grantee will achieve Y", if X never happens).
      • Some predictions were about grants that didn’t happen.

    We don't yet have systematic data to determine which of these reasons are more prevalent, but we may be able to say more about this in the future.

    • Overdue: Some predictions have overdue scores because they are associated with active grants that may be renewed in the future. In these cases, we don’t request scores from grant investigators until they write up the renewal grant. There may also be some scores we haven’t logged yet due to lack of capacity.
    • Missing End Date: Predictions with no end date can't be scored as False (because the event may still happen in the future). We’re currently working with grant investigators to log reasonable end dates for these.

  5. [5] We’re leaving out focus areas with less than $10M moved in the subsequent analyses. The excluded focus areas are South Asian Air Quality, History of Philanthropy, and Global Health and Wellbeing.

  6. [6] This sentence and some other explanatory language in this report are borrowed from an internal guide about forecasting written by Luke Muehlhauser.

  7. [7] These intervals assume a uniform prior over (0, 1). This means that, for a bin with T true predictions and F false predictions, the intervals are calculated using a Beta(T+1, F+1) distribution.

  8. [8] Detailed calibration data for each bin are provided below. Note that intervals are open to the left and closed to the right; a 30% prediction would be included in the 20-30 bin, but a 20% prediction would be included in the 10-20 bin.

    Confidence [%] True False Total
    0-10 5 39 44
    10-20 10 32 42
    20-30 20 53 73
    30-40 24 36 60
    40-50 69 82 151
    50-60 64 36 100
    60-70 86 44 130
    70-80 65 29 94
    80-90 34 7 41
    90-100 5 3 8

  9. [9] However, given that there is high variance in calibration across predictors, this may not be the best idea in all cases. For personal advice, predictors may wish to refer to their own calibration curve, or their team's curve.

  10. [10] A score of 0.25 is a reasonable baseline in our case because the base rate for past predictions happens to be very close to 50%. This means that predictors in the future could state 50% confidence on all predictions and, assuming the base rate stays the same (i.e. the population of questions that predictors sample from is stable over time), get close to perfect calibration without achieving any resolution.

  11. [11] For comparison, first-year participants in the Good Judgment Project (GJP) that were not given any training got a score of 0.21 (appears as 0.42 in table 4 here; Tetlock et al. scale their Brier score such that, for binary questions, we'd need to multiply our scores by 2 to get numbers with the same meaning). The Metaculus community averages 0.150 on binary questions as of this writing (May 2022). Both comparisons have very obvious caveats: the population of questions on GJP or Metaculus is very different from ours and both platforms calculate average Brier scores over time, taking into account updates to the initial forecast, while our grant investigators only submit one forecast and never try to refine it later.

  12. [12] For a base rate of 50%, resolution ranges from 0 (worst) to 0.25 (best). OP’s resolution is 0.037.

  13. [13] A caveat about this data: I'm taking the difference between 'End Date' (i.e. when a prediction is ready to be assessed) and 'Investigation Close Date' (the date the investigator submitted their request for conditional approval). This underestimates the time span between forecast and resolution because predictions are made before the investigation closes. This explains the fact that some time deltas are slightly negative. The most likely explanation for this is that the grant investigator wrote the prediction long before submitting the write-up for conditional approval.

  14. [14] This is in line with evidence from GJP and (less so) Metaculus showing that accuracy drops as time until question resolution increases. However, note that the opposite holds for PredictionBook, i.e. Brier scores tend to get better the longer the time horizon. Our working hypothesis to explain this paradoxical result is that, when users get to select the questions they forecast on (as they do on PredictionBook), they will only pick “easy” long-range questions. When the questions are chosen by external parties (as in GJP), they tend to be more similar in difficulty across time horizons. Metaculus sits somewhere in the middle, with community members posting most questions and opening them to the public. We may be able to test this hypothesis in the future by looking at data from Hypermind, which should fall closer to GJP than to the others because questions on the platform are commissioned by external parties.

  15. [15] This selection effect could come about through several mechanisms. One such mechanism could be picking well-defined processes more often in long-range forecasts than in short-range ones. In those cases, what matters is not the calendar time elapsed between start and end but the number and complexity of steps in the process. For example, a research grant may contain predictions about the likely output of that research (some finding or publication) that can't be scored until the research has been conducted. If the research was delayed for some reason, or if it happens earlier than expected due to e.g. a sudden influx of funding, that doesn't change the intrinsic difficulty of predicting anything about the research outcomes themselves.

Topics: